| Type: | Package |
| Title: | Interpolate Munsell Renotation Data from Hue Value/Chroma to CIE/RGB |
| Version: | 3.2-0 |
| Encoding: | UTF-8 |
| Date: | 2025-06-17 |
| Description: | Methods for interpolating data in the Munsell color system following the ASTM D-1535 standard. Hues and chromas with decimal values can be interpolated and converted to/from the Munsell color system and CIE xyY, CIE XYZ, CIE Lab, CIE Luv, or RGB. Includes ISCC-NBS color block lookup. Based on the work by Paul Centore, "The Munsell and Kubelka-Munk Toolbox". |
| License: | GPL (≥ 3) |
| LazyLoad: | yes |
| LazyData: | yes |
| Depends: | R (≥ 3.5.0) |
| Imports: | rootSolve, spacesRGB, spacesXYZ (≥ 1.6-0), logger |
| Suggests: | microbenchmark, mgcv, knitr, rmarkdown, colorSpec (≥ 1.8-0), flextable, OxSR |
| Author: | Jose Gama [aut, trl], Paul Centore [aut, cph], Glenn Davis [aut, cre] |
| Maintainer: | Glenn Davis <gdavis@gluonics.com> |
| Repository: | CRAN |
| NeedsCompilation: | no |
| VignetteBuilder: | knitr |
| BuildVignettes: | yes |
| Packaged: | 2025-06-17 16:18:04 UTC; Glenn |
| Date/Publication: | 2025-06-18 04:40:11 UTC |
Centroid Notations for the Revised ISCC-NBS Color-Name Blocks
Description
CentroidsISCCNBS is a table with the centroids
of the revised ISCC-NBS Color-Name Blocks, taken from Kelly (1958)
Format
This data.frame has 267 rows and these columns:
- Number
ISCC-NBS number (an integer from 1 to 267)
- Name
ISCC-NBS name
- MunsellSpec
Munsell specification of the centroid of the block a (character string)
Details
The earliest paper I am aware of is by Nickerson, et. al. in 1941.
After the big Munsell renotation in 1943, the name blocks were revised in 1955.
When the central colors were recomputed in
Kelly (1958), they were called the "Central Colors",
though the text makes it clear that most are truly centroids,
which were computed from the centroid of an "elementary shape",
which is a "sector of a right cylindrical annulus".
For the "peripheral blocks" of high chroma, the centroids were
"estimated graphically by plotting the MacAdam limits".
In Kelly (1965) these were called "centroid colors",
and that is the name we will use here.
Contributor
Glenn Davis
References
Nickerson, Dorothy and Sidney M. Newhall. Central Notations for ISCC-NBS Color names. J Opt. Soc. Am. Vol 31 Iss. 9. pp. 597-591. 1941.
Newhall, Sidney M., Dorothy Nickerson, Deane B. Judd. Final Report of the O.S.A. Subcommitte on the Spacing of the Munsell Colors. Journal of the Optical Society of America. Vol. 33. No. 7. pp. 385-418. July 1943.
Kelly, Kenneth L. and Deane B. Judd The ISCC-NBS Method of Designating Colors and a Dictionary of Color Names. National Bureau of Standards Circular 553. Washington DC: US Government Printing Office. November 1, 1955.
Kelly, Kenneth Low. Central Notations for the Revised ISCC-NBS Color-Name Blocks. Journal of Research of the National Bureau of Standards. Research Paper 2911. Vol. 61 No. 5. pp. 427-431. November 1958.
Kelly, Kenneth Low. A Universal Color Language. Color Engineering. Vol. 3 No. 2. pp. 2-7. March-April, 1965.
Examples
print( CentroidsISCCNBS[ 1:5, ] )
## Number Name MunsellSpec
## 1 1 vivid pink 1.5R 7/13
## 2 2 strong pink 1.5R 7.5/9.1
## 3 3 deep pink 1.9R 6.0/11.1
## 4 4 light pink 2.5R 8.6/5.2
## 5 5 moderate pink 2.5R 7.2/5.2
Get ISCC-NBS Number and ISCC-NBS Name from Munsell HVC or Munsell Notation
Description
Get ISCC-NBS Number and ISCC-NBS Name from Munsell HVC or Munsell Notation.
Usage
ColorBlockFromMunsell( MunsellSpec ) Arguments
MunsellSpec |
a numeric Nx3 matrix or a vector that can be converted to
such a matrix.
Each row has Munsell HVC, where H is Hue Number,
and V and C are the standard Munsell Value and Chroma.
The Hue is automatically wrapped to the interval (0,100].
|
Details
The ISCC-NBS System is a partition of Munsell Color Solid into 267 color blocks.
Each block is a disjoint union of elementary blocks,
where an elementary block is defined
by its minimum and maximum limits in Hue, Value, and Chroma.
Some blocks are non-convex.
The peripheral blocks, of which there are 120,
have arbitrary large chroma and are considered semi-infinite for this function;
there is no consideration of the MacAdam limits.
For each query vector HVC,
the function searches a private data.frame with 932 elementary blocks,
for the one elementary block that contains it.
Value
a data.frame with N rows and these columns:
HVC |
the input Nx3 matrix, or such a matrix converted from Munsell notation |
Number |
the corresponding ISCC-NBS color number - an integer from 1 to 267 |
Name |
the corresponding ISCC-NBS color name - a character string |
Centroid |
the centroid of the block in Munsell Notation - a character string; see |
The rownames are set to the input MunsellSpec.
History
The Munsell Book of Color was published in 1929. The first ISCC-NBS partition, in 1939, had 319 blocks and names (including 5 neutrals). There were no block numbers. The aimpoints of the Munsell samples were thoroughly revised in 1943. The ISCC-NBS partition was revised in 1955, and this is the version used here.
Future Work
It might be useful to compute the distance from the query point to the boundary of the containing color block.
Author(s)
Glenn Davis
References
Munsell Color Company, A.H. Munsell, and A.E.O. Munsell. Munsell book of color: defining, explaining, and illustrating the fundamental characteristics of color. 1929.
Judd, Deane B. and Kenneth L. Kelly. Method of Designating Colors. Journal of Research of the National Bureau of Standards. Research Paper 1239. Volume 23 Issue 3. pp. 355-385. September 1939.
Newhall, Sidney M., Dorothy Nickerson, Deane B. Judd. Final Report of the O.S.A. Subcommitte on the Spacing of the Munsell Colors. Journal of the Optical Society of America. Vol. 33. No. 7. pp. 385-418. July 1943.
Kelly, Kenneth L. and Deane B. Judd The ISCC-NBS Method of Designating Colors and a Dictionary of Color Names. National Bureau of Standards Circular 553. Washington DC: US Government Printing Office. November 1, 1955.
See Also
Examples
ColorBlockFromMunsell( c( "3R 8/3", "7.4YR 3/4" ) )
## HVC.H HVC.V HVC.C Number Name Centroid
## 3R 8/3 3.0 8.0 3.0 4 light pink 2.5R 8.6/5.2
## 7.4YR 3/4 17.4 3.0 4.0 58 moderate brown 5.5YR 3.5/3.9
Convert Colorlab Munsell Format to Munsell HVC
Description
Convert Colorlab Munsell Format to Munsell HVC
Usage
ColorlabFormatToMunsellSpec( HVCH )
Arguments
HVCH |
a numeric Nx4 matrix, or a vector that can be converted to such a matrix, by row.
Each row of the matrix contains an HVCH vector. |
Details
Colorlab Munsell format uses 4 numbers.
Hue Step, in the interval (0,10], or 0 for neutrals
Munsell Value, in the interval (0,10]
Munsell Chroma, non-negative
Hue Index, an integer from 1 to 10, or 0 for neutrals
Value
an Nx3 matrix, with each row an HVC vector.
Value and Chroma are simply copied unchanged.
The complex part is conversion of Colorlab Hue Step and Hue Index
to Hue Number.
For neutrals, both Hue Step and Hue Index are ignored.
Invalid input values, such as a Hue Index that is not
an integer from 0 to 10 (except for neutrals), are converted to NAs.
The rownames of the input are copied to the output,
but if these are NULL, the rownames are set to the Munsell notations.
Author(s)
Jose Gama and Glenn Davis
References
Color Processing Toolbox. Colorlab 1.0. https://www.uv.es/vista/vistavalencia/software/colorlab.html
See Also
Examples
ColorlabFormatToMunsellSpec( c( 3.2,3,2,1, 2,5.1,0,0, 2,5.1,0.1,0 ) )
## H V C
## 3.20B 3.00/2.00 63.2 3.0 2
## N 5.10/ 0.0 5.1 0
## <NA> NA NA NA
Convert Munsell Notation to numerical Munsell HVC
Description
Convert Munsell Notation to numerical Munsell HVC
Usage
HVCfromMunsellName( MunsellName )
MunsellHVC( MunsellName )
HueNumberFromString( HueString )
Arguments
MunsellName |
a character vector of length N > 0,
where each string should be a valid Munsell notation, e.g.
|
HueString |
a character vector of length N > 0,
where each string should be the initial hue part of a Munsell notation,
e.g. '4.5GY', '2.5R', '10.3B', etc.
Whitespace is optional and ignored.
Neutrals, denoted by |
Value
HVCfromMunsellName()
returns a numeric Nx3 matrix with HVC in the rows.
For neutral colors, both H and C are set to 0.
If a string cannot be parsed, the entire row is set to NAs.
The rownames are set to MunsellName.
MunsellHVC()
returns a character Nx3 matrix with HVC in the rows,
and is there for backward compatibility with older versions of the package.
For neutral colors, H is set to 'N' and C is set to '0'.
HueNumberFromString() returns the hue number H (in (0,100]).
If the string cannot be parsed, or the color is neutral, the output is set to NA.
For all functions the Hue Number is wrapped to (0,100].
Note
Ever since the Munsell Book of Color (1929), the Munsell hue circle has been divided into 5 principal hues and 5 intermediate hues, to define a total of 10 arcs. Each of these hues has been assigned a 10-point scale, with 5 at the midpoint of the arc. Moreover, the hue "origin" has been at '10RP'. So a 100-point scale (with no letters) for the entire hue circle is obvious and trivial to construct, but I have been unable to determine the first explicit mention of such a scale. The earliest I have have found is from Nimeroff (1968), Figures 20 and 21 on page 27.
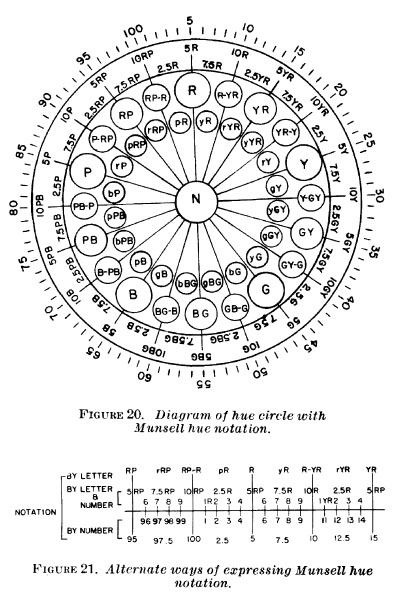
There is a reference to ASTM D 1535 in the References of Nimeroff,
but it is not dated, and the 2 figures are not attributed to it.
There was an ASTM D 1535 in 1968 but I have not been able to locate it;
it is possible that the 100-point scale first appeared in ASTM D-1535 (1968),
or even earlier in ASTM D 1525-58T (1958).
Interestingly, in the Atlas of the Munsell Color System (1915) there were only
5 principal hues (with no intermediate hues) and each of the 5 arcs was assigned a 10-point scale.
If the entire hue circle of 1915 were assigned a scale, it would have been a 50-point scale.
Author(s)
Glenn Davis
References
Nimeroff, I. Colorimetry. National Bureau of Standards Monograph 104. January 1968. 35 cents.
ASTM D 1535-80. Standard Practice for Specifying Color by the Munsell System. 1980.
Munsell Book of Color: defining, explaining, and illustrating the fundamental characteristics of color. Munsell Color Co. 1929.
Atlas of the Munsell Color System. Malden, Mass., Wadsworth, Howland & Co., inc., Printers. 1915.
See Also
MunsellNameFromHVC(),
HueStringFromNumber()
Examples
HVCfromMunsellName( c( "4.2P 2.9/3.8", "N 2.3/", "N 8.9/0" ) )
## H V C
## 4.2P 2.9/3.8 84.2 2.9 3.8
## N 2.3/ 0.0 2.3 0.0
## N 8.9/0 0.0 8.9 0.0
HueNumberFromString( c('4B','4.6GY','10RP','N') )
## [1] 64.0 34.6 100.0 NA
Test xyY Coordinates for being Inside the MacAdam Limits
Description
Test xyY Coordinates for being Inside the MacAdam Limits for Illuminants C and D65
Usage
IsWithinMacAdamLimits( xyY, Illuminant='C' )
Arguments
xyY |
a numeric Nx3 matrix with CIE xyY coordinates in the rows, or a vector that can be converted to such a matrix, by row. The reference white is asssumed to have Y=100. |
Illuminant |
either |
Details
The MacAdam Limit is the boundary of the optimal color solid (also called the Rösch Farbkörper), in XYZ coordinates. The optimal color solid is convex and depends on the illuminant. Points on the boundary of the solid are called optimal colors. It is symmetric about the midpoint of the segment joining black and white (the 50% gray point). It can be expressed as a zonohedron - a convex polyhedron with a special form; for details on zonohedra, see Centore.
For each of the 2 illuminants, a zonohedron Z is pre-computed
(and stored in sysdata.rda).
The wavelengths used are 380 to 780 nm with 5nm step (81 wavelengths).
Each zonohedron has 81*80=6480 parallelogram faces, though some of them are coplanar.
Z is expressed as the intersection of 6480 halfspaces.
The plane equation of each parallelogram is pre-computed,
but redundant ones are not removed (in this version).
For testing a query point xyY, a pseudo-distance metric \delta is used.
Let the zonohedron Z be the intersection of the halfspaces
⟨ h_i,x ⟩ \le b_i ~~ i=1,...,n,
where each h_i is a unit vector.
The point xyY is converted to XYZ, and \delta(XYZ) is computed as:
\delta(XYZ) := max( ⟨ h_i,XYZ ⟩ - b_i )
where the maximum is taken over all i=1,...,n.
This calculation can be optimized;
because the zonohedron is centrally symmetric, only half of the planes actually have to be stored,
and this cuts the memory and processing time in half.
It is clear that XYZ is within the zonohedron iff \delta(XYZ) \le 0,
and that XYZ is on the boundary iff \delta(XYZ)=0.
This pseudo-distance is part of the returned data.frame.
An interesting fact is that if \delta(XYZ)>0,
then \delta(XYZ) \le dist(XYZ,Z),
with equality iff the segment from XYZ to the
point z on the boundary of Z closest to XYZ is
normal to one of the faces of Z that contains z.
This is why we call \delta a pseudo-distance.
Another interesting fact is that if \delta(XYZ) \le 0,
then \delta(XYZ) = -min( \Psi_Z(u) - ⟨ u,XYZ ⟩ ),
where the minimum is taken over all unit vectors u and
where \Psi_Z is the support function of Z.
Value
A data.frame with N rows and these columns:
within |
a logical which is |
delta |
the pseudo-distance |
The row names of the output value are set equal to the row names of xyY.
Author(s)
Glenn Davis and Jose Gama
References
Centore, Paul. A zonohedral approach to optimal colours. Color Research & Application. Vol. 38. No. 2. pp. 110-119. April 2013.
Rösch, S. Darstellung der Farbenlehre für die Zwecke des Mineralogen. Fortschr. Mineral. Krist. Petrogr. Vol. 13 No. 143. 1929.
MacAdam, David L. Maximum Visual Efficiency of Colored Materials. Journal of the Optical Society of America. Vol 25, No. 11. pp. 361-367. November 1935.
Wikipedia. Support Function. https://en.wikipedia.org/wiki/Support_function
Examples
IsWithinMacAdamLimits( c(0.6,0.3,10, 0.6,0.3,20, 0.6,0.3,30, 0.6,0.3,40 ), 'C' )
## within delta
## 1 TRUE -1.941841
## 2 TRUE -1.332442
## 3 FALSE 3.513491
## 4 FALSE 12.826172
Convert CIE Lab coordinates to Munsell HVC
Description
LabToMunsell Converts CIE Lab coordinates to Munsell HVC,
by interpolating over the extrapolated Munsell renotation data
Usage
LabToMunsell( Lab, white='D65', adapt='Bradford', ... )Arguments
Lab |
CIE Lab coordinates. An Nx3 matrix, or a vector that can be converted to such a matrix. Each row of the matrix has Lab. |
white |
XYZ for the source white - a numeric 3-vector with scaling irrelevant.
|
adapt |
method for chromatic adaptation, see |
... |
other parameters passed to |
Details
The conversion is done in these steps.
Lab → XYZ using
spacesXYZ::XYZfromLab()with the givenwhite.XYZ is then adapted from the given
whiteto Illuminant C using the givenadaptmethod.XYZ → HVC using
XYZtoMunsell().
Value
An Nx3 matrix with the Munsell HVC coordinates in each row. The rownames are set to those of Lab.
Note
The case of the letter 't' in the function name was recently changed from lower to upper.
The function LabtoMunsell() is equivalent but deprecated and provided for a limited time.
Author(s)
Jose Gama and Glenn Davis
References
Paul Centore 2014 The Munsell and Kubelka-Munk Toolbox https://www.munsellcolourscienceforpainters.com/MunsellAndKubelkaMunkToolbox/MunsellAndKubelkaMunkToolbox.html
See Also
MunsellToLab(),
XYZtoMunsell(),
spacesXYZ::standardXYZ(),
spacesXYZ::CAT(),
spacesXYZ::XYZfromLab()
Examples
LabToMunsell( c(74.613450, -20.4, 10.1, 80, 0, 0) )
## H V C
## 3.1G 7.4/3.6 43.13641 7.379685 3.62976
## N 7.9/ 0.00000 7.945314 0.00000
Convert CIE Luv coordinates to Munsell HVC
Description
LuvToMunsell Converts CIE Luv coordinates to Munsell HVC,
by interpolating over the extrapolated Munsell renotation data
Usage
LuvToMunsell( Luv, white='D65', adapt='Bradford', ... ) Arguments
Luv |
CIE Luv coordinates An Nx3 matrix, or a vector that can be converted to such a matrix. Each row of the matrix has Luv. |
white |
XYZ for the source white - a numeric 3-vector with scaling irrelevant.
|
adapt |
method for chromatic adaptation, see Details |
... |
other parameters passed to |
Details
The conversion is done in these steps:
Luv → XYZ using
spacesXYZ::XYZfromLuv()with the givenwhite.XYZ is then adapted from the given
whiteto Illuminant C using the given chromatic adaptation method, seespacesXYZ::CAT().XYZ → HVC using
XYZtoMunsell()
Value
An Nx3 matrix with the Munsell HVC coordinates in each row. The rownames are set to those of Luv.
Note
The case of the letter 't' in the function name was recently changed from lower to upper.
The function LuvtoMunsell() is equivalent but deprecated and provided for a limited time.
Author(s)
Jose Gama and Glenn Davis
References
Paul Centore 2014 The Munsell and Kubelka-Munk Toolbox https://www.munsellcolourscienceforpainters.com/MunsellAndKubelkaMunkToolbox/MunsellAndKubelkaMunkToolbox.html
See Also
XYZtoMunsell(),
spacesXYZ::XYZfromLuv(),
spacesXYZ::standardXYZ(),
spacesXYZ::CAT()
Examples
LuvToMunsell( c( 74.613450, -5.3108, 10.6, 55, 0, 0 ) )
## H V C
## 8.7GY 7.4/1.2 38.6599 7.383948 1.229376
## N 5.4/ 0.0000 5.395003 0.000000
The Munsell HVC to xy 3D Lookup Table
Description
This is the discrete data for the Munsell Renotation System, which is often considered to be the most perceptually uniform color atlas. It was created by the NBS and OSA from "3,000,000 color judgments" by 40 observers.
Format
A data frame with 4995 observations of the following 6 variables.
Hthe Munsell Hue. EachHis a multiple of 2.5 and in the interval (0,100].Vthe Munsell Value. EachVis an integer from 1 to 10, or one of 0.2, 0.4, 0.6, 0.8Cthe Munsell Chroma. EachCis a positive even integer.xthe x chromaticity coordinate, for Illuminant C.ythe y chromaticity coordinate, for Illuminant C.reala logical value. IfTRUEthen x,y were published, otherwise they have been extrapolated.
Note that the luminance factor Y is *not* here,
since Y is a simple function of V,
see YfromV().
Details
All the (x,y) data here comes from the file all.dat downloaded from
Rochester Institute of Technology, see Source.
The file real.dat is a subset, and contains the (x,y) published
in Newhall, et. al. (1943).
These rows have real=TRUE and are only for Value \ge 1.
There are 2734 of these.
Similarly, for Value<1 (very dark colors), (x,y) data from
the paper Judd et. al. (1956) also have real=TRUE.
There are 355 of these.
So all.dat has 4995 colors,
of which 2734+355=3089 are "real" colors,
and the remaining 1906 are extrapolated.
I am confident that the extrapolation was done by
Schleter et. al. (1958) at the NBS,
and put online by the Rochester Institute of Technology.
For more details, and the abstract of the 1958 article,
see the munsellinterpol User Guide.
Note
For the purpose of this package, I have found that the extrapolated (x,y)
for V\ge1 work well.
But for V<1 they did not work so well, and I was able to get better results with
my own extrapolation.
Moreover, to get reliable results in this package for high Chroma,
it was necessary to extrapolate past the data in all.dat.
Author(s)
Glenn Davis
Source
Rochester Institute of Technology. Program of Color Science. Munsell Renotation Data. https://www.rit.edu/science/munsell-color-lab
References
Newhall, Sidney M., Dorothy Nickerson, Deane B. Judd. Final Report of the O.S.A. Subcommitte on the Spacing of the Munsell Colors. Journal of the Optical Society of America. Vol. 33. No. 7. pp. 385-418. July 1943.
Judd, Deane B. and Gunter Wyszecki. Extension of the Munsell Renotation System to Very Dark Colors. Journal of the Optical Society of America. Vol. 46. No. 4. pp. 281-284. April 1956.
Schleter, J. C, D. B. Judd, D. B., H. J. Keegan. Extension of the Munsell Renotation System (Abstract). J. Opt. Soc. Am. Vol 48. Num. 11. pp. 863-864. presented at the Forty-Third Annual Meeting of the Optical Society of America. Statler Hilton Hotel, Detroit, Michigan. October 9, 10, and 11, 1958.
See Also
YfromV()
Examples
str(Munsell2xy)
## 'data.frame': 4995 obs. of 6 variables:
## $ H : num 32.5 35 37.5 37.5 40 40 42.5 42.5 45 45 ...
## $ V : num 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 ...
## $ C : num 2 2 2 4 2 4 2 4 2 4 ...
## $ x : num 0.713 0.449 0.262 -0.078 0.185 -0.257 0.144 -0.235 0.117 -0.209 ...
## $ y : num 1.414 1.145 0.837 2.16 0.676 ...
## $ real: logi FALSE FALSE FALSE FALSE TRUE FALSE ...
Convert Munsell Numeric to Munsell String Notation
Description
Convert Munsell Numeric to Munsell String Notation
Usage
MunsellNameFromHVC( HVC, format='g', digits=2 )
HueStringFromNumber( Hue, format='g', digits=2 )
Arguments
HVC |
a numeric Nx3 matrix or a vector that can be converted to such a matrix. Each row has an HVC vector, where H is Hue Number, and V and C are the standard Munsell Value and Chroma. The Hue is automatically wrapped to the interval (0,100]. |
Hue |
a numeric vector of Hue Numbers, which are automatically wrapped to the interval (0,100]. |
format |
determines the meaning of the argument |
digits |
when |
Value
Both functions return a character vector of length N.
MunsellNameFromHVC() returns the full notation.
HueStringFromNumber() returns just initial the hue part;
which is useful for labeling plots.
Note
If format='f', then Chroma is first rounded to to the given digits.
Chromas close to 0 may then become 0 and be displayed as a neutral, see Examples.
The width argument of formatC() is always set to 1,
to suppress leading spaces.
Author(s)
Glenn Davis
References
ASTM D 1535-97. Standard Practice for Specifying Color by the Munsell System. 1997
See Also
formatC(),
HVCfromMunsellName(),
HueNumberFromString()
Examples
MunsellNameFromHVC( c(39,5.1,7.3, 0,5.1234,0.003 ) )
## [1] "9GY 5.1/7.3" "10RP 5.1/0.003"
MunsellNameFromHVC( c(39,5.1,7.34, 0,5.1234,0.003 ), format='f' )
## [1] "9.00GY 5.10/7.34" "N 5.10/"
HueStringFromNumber( seq( 2.5, 100, by=2.5 ) ) # make nice labels for a plot
## [1] "2.5R" "5R" "7.5R" "10R" "2.5YR" "5YR" "7.5YR" "10YR" "2.5Y"
## [10] "5Y" "7.5Y" "10Y" "2.5GY" "5GY" "7.5GY" "10GY" "2.5G" "5G"
## [19] "7.5G" "10G" "2.5BG" "5BG" "7.5BG" "10BG" "2.5B" "5B" "7.5B"
## [28] "10B" "2.5PB" "5PB" "7.5PB" "10PB" "2.5P" "5P" "7.5P" "10P"
## [37] "2.5RP" "5RP" "7.5RP" "10RP"
Convert Munsell Specification to Colorlab Format
Description
Convert Munsell Specification to Colorlab Format
Usage
MunsellSpecToColorlabFormat( MunsellSpec )
Arguments
MunsellSpec |
a numeric Nx3 matrix, or a vector that can be converted to such a matrix, by row.
Each row of the matrix contains an HVC vector.
H is automatically wrapped to the interval (0,100]. |
Details
Colorlab Munsell format uses 4 numbers.
Hue Step, in the interval (0,10], or 0 for neutrals. In Colorlab documentation it is called the hue shade. It is also the Hue Number H mod 10 (unless H is an exact multiple of 10).
Munsell Value, in the interval [0,10]
Munsell Chroma, non-negative
Hue Index, an integer from 1 to 10, or 0 for neutrals. This index defines the principal hue, see Details.
Value
an Nx4 matrix, with rows as described in Details.
Value and Chroma are simply copied unchanged.
The complex part is conversion of Hue Number to Colorlab Hue Step and Hue Index.
If Chroma is 0, both the Hue Step and Hue Index are set to 0.
Invalid input values are converted to NAs.
If the input is a character vector,
the rownames of the returned matrix are set to that vector.
Note
The Colorlab format is closer to the
Munsell Book of Color (1929) than HVC.
In the book the hue circle is divided into 10
principal hues - 5 simple and 5 compound.
The 10 hue labels are: R, YR, Y, GY G, BG, B, PB, P
(simple are 1 letter and compound are 2 letters).
In Colorlab these labels are replaced by the Hue Index.
WARNING: In the Munsell System, see Cleland, there is a different Hue Index -
R is 1, YR is 2, ..., P is 10.
The Colorlab index has a different origin, and goes around the circle in a different
direction !
Each one of these major hues corresponds to an arc on the circle,
with a 10-point hue scale.
The midpoint of the arc has hue step = 5.
Fortunately this 10-point hue scale is exactly the same as the Colorlab Hue Step.
Author(s)
Jose Gama and Glenn Davis
References
Color Processing Toolbox. Colorlab 1.0. https://www.uv.es/vista/vistavalencia/software/colorlab.html
Cleland, T. M. A Practical description of the Munsell Color System with Suggestions for its Use. (1921)
See Also
HVCfromMunsellName(),
ColorlabFormatToMunsellSpec()
Examples
MunsellSpecToColorlabFormat( c(100,5,5, 10,3,4, 90,4,3, 77,1,2, 66,2,0, 0,1,2 ) )
## HN V C HI
## 10.00RP 5.00/5.00 10 5 5 8
## 10.00R 3.00/4.00 10 3 4 7
## 10.00P 4.00/3.00 10 4 3 9
## 7.00PB 1.00/2.00 7 1 2 10
## N 2.00/ 0 2 0 0
## 10.00RP 1.00/2.00 10 1 2 8
Convert a Munsell specification to CIE Lab coordinates
Description
MunsellToLab Converts a
Munsell specification to CIE Lab coordinates, by interpolating over the
extrapolated Munsell renotation data
Usage
MunsellToLab( MunsellSpec, white='D65', adapt='Bradford', ... ) Arguments
MunsellSpec |
a numeric Nx3 matrix with HVC values in the rows, or a vector that can be converted to such a matrix, by row. |
white |
XYZ for the source white - a numeric 3-vector with scaling irrelevant.
|
adapt |
method for chromatic adaptation, see |
... |
other parameters passed to |
Details
The conversion is done in these steps:
HVC → XYZ using
MunsellToXYZ()XYZ is adapted from Illuminant C to the given
whiteusingspacesXYZ::adaptXYZ()and the given chromatic adaptation methodXYZ → Lab using
spacesXYZ::LabfromXYZ()with the givenwhite
Value
An Nx3 matrix with the Lab coordinates in each row.
The rownames of Lab are copied from the input HVC matrix,
unless the rownames are NULL and
then the output rownames are the Munsell notations for HVC.
Author(s)
Jose Gama and Glenn Davis
References
Paul Centore 2014 The Munsell and Kubelka-Munk Toolbox https://www.munsellcolourscienceforpainters.com/MunsellAndKubelkaMunkToolbox/MunsellAndKubelkaMunkToolbox.html
See Also
LabToMunsell(),
MunsellToXYZ(),
spacesXYZ::LabfromXYZ(),
spacesXYZ::standardXYZ(),
spacesXYZ::adaptXYZ(),
spacesXYZ::CAT()
Examples
MunsellToLab( c('7.6P 8.9/2.2', 'N 5/' ) )
## L a b
## 7.6P 8.9/2.2 89.19097 5.09879 -3.250468
## N 5/ 51.00375 0.00000 0.000000
Convert a Munsell specification to CIE Luv coordinates
Description
MunsellToLuv Converts a
Munsell specification to CIE Luv coordinates, by interpolating over the
extrapolated Munsell renotation data
Usage
MunsellToLuv( MunsellSpec, white='D65', adapt='Bradford', ... ) Arguments
MunsellSpec |
a numeric Nx3 matrix with HVC values in the rows, or a vector that can be converted to such a matrix, by row. |
white |
XYZ for the source white - a numeric 3-vector with scaling irrelevant.
|
adapt |
method for chromatic adaptation, see |
... |
other parameters passed to |
Details
The conversion is done in these steps:
HVC → XYZ using
MunsellToXYZ()XYZ is adapted from Illuminant C to the given
whiteusingspacesXYZ::adaptXYZ()with the given chromatic adaptation methodXYZ → Luv using
spacesXYZ::LuvfromXYZ()with the givenwhite
Value
An Nx3 matrix with the Luv coordinates in each row.
The rownames of Luv are copied from the input HVC matrix,
unless the rownames are NULL and
then the output rownames are the Munsell notations for HVC.
Author(s)
Jose Gama and Glenn Davis
References
Paul Centore 2014 The Munsell and Kubelka-Munk Toolbox https://www.munsellcolourscienceforpainters.com/MunsellAndKubelkaMunkToolbox/MunsellAndKubelkaMunkToolbox.html
See Also
LuvToMunsell(),
MunsellToXYZ(),
spacesXYZ::standardXYZ(),
spacesXYZ::CAT(),
spacesXYZ::adaptXYZ(),
spacesXYZ::LuvfromXYZ()
Examples
MunsellToLuv( c('7.6P 8.9/2.2', 'N 5/' ) )
## L u v
## 7.6P 8.9/2.2 89.19097 5.247155 -5.903808
## N 5/ 51.00375 0.000000 0.000000
Convert a Munsell specification to RGB coordinates
Description
MunsellToRGB Converts a
Munsell specification to RGB coordinates, by interpolating over the
extrapolated Munsell renotation data
Usage
MunsellToRGB( MunsellSpec, space='sRGB', which='scene', maxSignal=255,
adapt='Bradford', ... ) Arguments
MunsellSpec |
a numeric Nx3 matrix with HVC values in the rows, or a vector that can be converted to such a matrix, by row. |
space |
the name of an installed RGB space.
Spaces |
which |
either |
maxSignal |
maximum of the non-linear signal RGB; Other popular values are 1, 100, 1023, and 65535 |
adapt |
method for chromatic adaptation, see |
... |
other parameters passed to |
Details
The conversion is done with these steps:
HVC → xyY using
MunsellToxyY()with.... This xyY is for Illuminant C.xyY → XYZ using
spacesXYZ::XYZfromxyY()XYZ is adapted from Illuminant C to the white-point (with
which) of the RGBspace, usingspacesXYZ::adaptXYZ(), with the given chromatic adaptation methodadaptXYZ → RGB using
spacesRGB::RGBfromXYZ()with the givenspace,which, andmaxSignal
Value
a data.frame with these columns:
SAMPLE_NAME |
a character N-vector equal to the original |
xyY |
an Nx3 matrix with xyY values in the rows, that are adapted to Illuminant C.
This is an intermediate result that is sometimes useful, e.g. it can be passed
to |
RGB |
an Nx3 matrix with non-linear RGB signal values in the rows.
All values are clamped to the appropriate cube, e.g. |
OutOfGamut |
logical vector, TRUE means the result was out of gamut (the cube) before clamping it |
In case of error, it returns NULL.
Author(s)
Jose Gama and Glenn Davis
References
Paul Centore 2014 The Munsell and Kubelka-Munk Toolbox https://www.munsellcolourscienceforpainters.com/MunsellAndKubelkaMunkToolbox/MunsellAndKubelkaMunkToolbox.html
See Also
MunsellToXYZ(),
IsWithinMacAdamLimits(),
spacesRGB::installRGB(),
spacesRGB::RGBfromXYZ(),
spacesXYZ::XYZfromxyY(),
spacesXYZ::CAT()
Examples
MunsellToRGB( c('7.6P 8.9/2.2', 'N 3/'), space='AdobeRGB' )
## SAMPLE_NAME xyY.x xyY.y xyY.Y RGB.R RGB.G RGB.B OutOfGamut
## 1 7.6P 8.9/2.2 0.3109520 0.3068719 74.6134498 227.72419 220.18659 229.23297 FALSE
## 2 N 3/ 0.3101000 0.3163000 6.3911778 73.01793 73.01793 73.01793 FALSE
Convert a Munsell specification to CIE XYZ coordinates
Description
MunsellToXYZ Converts a
Munsell specification to XYZ coordinates, by interpolating over the
extrapolated Munsell renotation data
Usage
MunsellToXYZ( MunsellSpec, ... ) Arguments
MunsellSpec |
a numeric Nx3 matrix with HVC values in the rows, or a vector that can be converted to such a matrix, by row. |
... |
other parameters passed to |
Details
The conversion is done in these steps:
HVC → xyY using
MunsellToxyY()and.... This xyY is for Illuminant C.xyY → XYZ using
spacesXYZ::XYZfromxyY()
Value
an Nx3 matrix with XYZ values in the rows.
The rownames of XYZ are copied from the input HVC matrix,
unless the rownames are NULL and
then the output rownames are the Munsell notations for HVC.
Note that these XYZ values are for viewing under Illuminant C, with Y=100.
There is no chromatic adaptation.
Author(s)
Jose Gama and Glenn Davis
References
Paul Centore 2014 The Munsell and Kubelka-Munk Toolbox https://www.munsellcolourscienceforpainters.com/MunsellAndKubelkaMunkToolbox/MunsellAndKubelkaMunkToolbox.html
See Also
MunsellToxyY(),
spacesXYZ::XYZfromxyY()
Examples
MunsellToXYZ('7.6P 8.9/2.2')
## X Y Z
## 7.6P 8.9/2.2 75.6055 74.61345 92.92308
Convert a Munsell specification to sRGB coordinates
Description
MunsellTosRGB Converts a
Munsell specification to non-linear sRGB coordinates, by interpolating over the
extrapolated Munsell renotation data
Usage
MunsellTosRGB( MunsellSpec, maxSignal=255, ... ) Arguments
MunsellSpec |
a numeric Nx3 matrix with HVC values in the rows, or a vector that can be converted to such a matrix, by row. |
maxSignal |
maximum of signal sRGB; Other popular values are 1, 100, 1023, and 65535 |
... |
other parameters passed to |
Details
The conversion is done in these steps.
HVC → xyY using
MunsellToxyY()and the given.... This xyY is for Illuminant C.xyY → XYZ using
spacesXYZ::XYZfromxyY()XYZ is adapted from Illuminant C to Illuminant D65 (from the sRGB standard) using
spacesXYZ::adaptXYZ()and the Bradford chromatic adaptation methodXYZ → sRGB using
spacesRGB::RGBfromXYZ()with the givenmaxSignal
Value
a data.frame with these columns:
SAMPLE_NAME |
the original |
xyY |
an Nx3 matrix with xyY values in the rows, that are adapted to Illuminant C.
This is an intermediate result that is sometimes useful, e.g. it can be passed
to |
RGB |
an Nx3 matrix with non-linear signal sRGB values in the rows.
All values are clamped to the appropriate cube, e.g. |
OutOfGamut |
logical vector, TRUE means the RGB result was out of gamut (the cube) before clamping it |
Note
The more general function MunsellToRGB() also performs this conversion.
The main reason to use MunsellTosRGB() is that it takes a little less time,
since the CAT (using the Bradford method) is precomputed during
base::.onLoad().
Author(s)
Jose Gama and Glenn Davis
References
Paul Centore 2014 The Munsell and Kubelka-Munk Toolbox https://www.munsellcolourscienceforpainters.com/MunsellAndKubelkaMunkToolbox/MunsellAndKubelkaMunkToolbox.html
See Also
MunsellToXYZ(),
MunsellToRGB(),
spacesXYZ::XYZfromxyY(),
spacesXYZ::CAT(),
spacesXYZ::adaptXYZ(),
spacesRGB::RGBfromXYZ(),
IsWithinMacAdamLimits()
Examples
MunsellTosRGB( c('7.6P 8.9/2.2', 'N 3/') )
## SAMPLE_NAME xyY.x xyY.y xyY.Y RGB.R RGB.G RGB.B OutOfGamut
## 1 7.6P 8.9/2.2 0.3109520 0.3068719 74.6134498 231.35746 221.14207 230.35011 FALSE
## 2 N 3/ 0.3101000 0.3163000 6.3911778 71.50491 71.50491 71.50491 FALSE
Convert Munsell HVC to xyY coordinates
Description
MunsellToxyY Converts Munsell HVC to xyY coordinates, by interpolating over the
extrapolated Munsell renotation data
Usage
MunsellToxyY( MunsellSpec, xyC='NBS', hcinterp='bicubic', vinterp='cubic',
YfromV='ASTM', warn=TRUE ) Arguments
MunsellSpec |
a numeric Nx3 matrix or a vector that can be converted to
such a matrix.
Each row has Munsell HVC, where H is Hue Number,
and V and C are the standard Munsell Value and Chroma.
The Hue is automatically wrapped to the interval (0,100].
| ||||||||||||||||
xyC |
a numeric 2-vector with xy chromaticity of Illuminant C. It can also be one of the strings in the first column of this table; it is then replaced by the corresponding xy in the second column.
The default | ||||||||||||||||
hcinterp |
either | ||||||||||||||||
vinterp |
either | ||||||||||||||||
YfromV |
passed as the parameter | ||||||||||||||||
warn |
if a chip cannot be mapped (usually because the Chroma is too large),
its x and y are set to |
Details
In case hcinterp='bicubic' or vinterp='cubic' a Catmull-Rom spline is used;
see the article Cubic Hermite spline.
This spline has the nice property that it is local and requires at most 4 points.
And if the knot spacing is uniform:
1) the resulting spline is C^1,
2) if the knots are on a line, the interpolated points are on the line too.
Value
a data.frame with these columns:
SAMPLE_NAME |
the original |
HVC |
the input Nx3 matrix, or the HVC matrix converted from the input Munsell notation |
xyY |
the computed output matrix, with CIE xyY coordinates of MunsellSpec illuminated by Illuminant C.
In case of error, x and y are set to |
Warning
Even when vinterp='cubic' the function HVC → xyY is not C^1
on the plane V=1.
This is because of a change in Value spacing:
when V\ge1 the Value spacing is 1, but when V\le1 the Value spacing is 0.2.
Note
When making plots in planes of constant Value,
option hcinterp='bicubic' makes fairly smooth ovals,
and hcinterp='bilinear' makes polygons.
The ovals are smooth even when vinterp='linear',
but the function is not class C^1 at the planes of integer Value.
To get a fully C^1 function (except at the neutrals and on the plane V=1),
hcinterp and vinterp must be set to the defaults.
Author(s)
Jose Gama and Glenn Davis
Source
Paul Centore 2014
The Munsell and Kubelka-Munk Toolbox
https://www.munsellcolourscienceforpainters.com/MunsellAndKubelkaMunkToolbox/MunsellAndKubelkaMunkToolbox.html
https://www.rit.edu/science/munsell-color-lab
https://www.rit-mcsl.org/MunsellRenotation/all.dat
https://www.rit-mcsl.org/MunsellRenotation/real.dat
References
Judd, Deane B. The 1931 I.C.I. Standard Observer and Coordinate System for Colorimetry. Journal of the Optical Society of America. Vol. 23. pp. 359-374. October 1933.
Newhall, Sidney M., Dorothy Nickerson, Deane B. Judd. Final Report of the O.S.A. Subcommitte on the Spacing of the Munsell Colors. Journal of the Optical Society of America. Vol. 33. No. 7. pp. 385-418. July 1943.
Kelly, Kenneth L. Kasson S. Gibson. Dorothy Nickerson. Tristimulus Specification of the Munsell Book of Color from Spectrophometric Measurements National Bureau of Standards RP1549 Volume 31. August 1943.
Judd, Deane B. and Günther Wyszecki. Extension of the Munsell Renotation System to Very Dark Colors. Journal of the Optical Society of America. Vol. 46. No. 4. pp. 281-284. April 1956.
National Television System Committee. [Report and Reports of Panel No. 11, 11-A, 12-19, with Some supplementary references cited in the Reports, and the Petition for adoption of transmission standards for color television before the Federal Communications Commission] (1953)
Rheinboldt, Werner C. and John P. Menard. Mechanized Conversion of Colorimetric Data to Munsell Renotations. Journal of the Optical Society of America. Vol. 50, Issue 8, pp. 802-807. August 1960.
Wikipedia. Cubic Hermite spline. https://en.wikipedia.org/wiki/Cubic_Hermite_spline
Paul Centore 2014 The Munsell and Kubelka-Munk Toolbox https://www.munsellcolourscienceforpainters.com/MunsellAndKubelkaMunkToolbox/MunsellAndKubelkaMunkToolbox.html
See Also
Examples
MunsellToxyY( '7.6P 8.9/2.2' )
## SAMPLE_NAME HVC.H HVC.V HVC.C xyY.x xyY.y xyY.Y
## 1 7.6P 8.9/2.2 87.6 8.9 2.2 0.3109520 0.3068719 74.6134498
Calculate the Nickerson Color Difference between two Colors
Description
Calculate the Nickerson Color Difference between two colors, given in Munsell HVC; see Nickerson.
Usage
NickersonColorDifference( HVC0, HVC1, symmetric=TRUE, coeffs=c(0.4,6,3) ) Arguments
HVC0 |
a numeric Nx3 matrix with HVC values in the rows, or a vector that can be converted to such a matrix, by row.
|
HVC1 |
a numeric Nx3 matrix with HVC values in the rows, or a vector that can be converted to such a matrix, by row.
|
symmetric |
if |
coeffs |
the coefficients for Hue, Value, and Chroma in the difference equation, see Details. The defaults are the ones used by Nickerson, but tweaking them is possible in special circumstances. The argument must have length 3 and all coefficents positive. |
Details
If HVC0=H_0,V_0,C_0 and If HVC1=H_1,V_1,C_1 then the original Nickerson formula is:
NCD(HVC0,HVC1) = 0.4 C_0 \Delta H ~+~ 6 \Delta V ~+~ 3 \Delta C
where \Delta H = |H_0 - H_1| (on the circle),
\Delta V = |V_0 - V_1| and
\Delta C = |C_0 - C_1| .
Unfortunately, if HVC0 and HVC1 are swapped, the color difference is different.
The first color is considered to be the reference color and the second one is the test color.
The difference is not symmetric.
Another problem is that the difference is not continuous when the second color is a neutral gray,
for rectangular coordinates on a plane of constant V.
Both of these problems are fixed with a slightly modified formula:
NCD(HVC0,HVC1) = 0.4 \min(C_0,C_1) \Delta H ~+~ 6 \Delta V ~+~ 3 \Delta C
For the first formula set symmetric=FALSE and for the second formula set symmetric=TRUE.
Value
A numeric N-vector with the pairwise differences,
i.e. between row i of HVC0 and row i of HVC1.
Author(s)
Jose Gama and Glenn Davis
References
Nickerson, Dorothy. The Specification of Color Tolerances. Textile Research. Vol 6. pp. 505-514. 1936.
Examples
NickersonColorDifference( '7.6P 8.9/2.2', '8P 8.2/3' )
## [1] 6.952
Convert RGB coordinates to Munsell HVC
Description
RGBtoMunsell Converts RGB coordinates to Munsell HVC,
by interpolating over the extrapolated Munsell renotation data
Usage
RGBtoMunsell( RGB, space='sRGB', which='scene', maxSignal=255, adapt='Bradford', ... ) Arguments
RGB |
a numeric Nx3 matrix with RGB coordinates in the rows, or a vector that can be converted to such a matrix, by row. These are non-linear display values, but they are not required to be integers. |
space |
the name of an installed RGB space.
Spaces |
which |
either |
maxSignal |
maximum value of signal RGB. Other popular values are 1, 100, 1023, and 65535. Even when 1, they are still taken to be non-linear signal values. |
adapt |
method for chromatic adaptation,
see |
... |
other parameters passed to |
Details
The conversion is done in these steps:
RGB → XYZ using
spacesRGB::XYZfromRGB()with the givenspace,which, andmaxSignalXYZ is adapted from the white-point (with
which) ofspaceto Illuminant C, usingspacesXYZ::adaptXYZ(), with the given chromatic adaptation methodadaptXYZ → HVC using
XYZtoMunsell()with...
Value
a numeric Nx3 matrix with HVC coordinates in the rows.
The rownames are copied from input RGB to output HVC, unless the rownames are NULL
when they are set to the Munsell notations for HVC.
In case of error, it returns NULL.
Author(s)
Jose Gama and Glenn Davis
References
Wikipedia. sRGB. https://en.wikipedia.org/wiki/SRGB.
Paul Centore 2014 The Munsell and Kubelka-Munk Toolbox https://www.munsellcolourscienceforpainters.com/MunsellAndKubelkaMunkToolbox/MunsellAndKubelkaMunkToolbox.html
See Also
XYZtoMunsell(),
spacesXYZ::CAT(),
spacesXYZ::adaptXYZ(),
spacesRGB::XYZfromRGB()
Examples
RGBtoMunsell( c(255,45,67) )
## H V C
## 5.4R 5.5/18 5.401135 5.477315 18.01984
RGBtoMunsell( c(255,45,67), space='Adobe' )
## H V C
## 5.9R 6.2/22 5.924749 6.214155 21.83907
Convert Munsell Value V to Luminance Factor Y, and back again
Description
Convert non-linear Munsell Value V to linear Luminance Factor Y, and back again
Usage
YfromV( V, which='ASTM' )
VfromY( Y, which='ASTM' )Arguments
V |
a numeric vector with elements in the interval [0,10] | |||||||||||||
Y |
a numeric vector with elements in the interval [0,100] | |||||||||||||
which |
one of the strings in the first column of this table
Partial matching is enabled, and it is case insensitive. |
Details
'Priest' is the earliest (1920) transfer function in this package.
It is implemented as:
V = sqrt(Y) ~~~~~~and~~~~~~ Y = V^2
One readily checks that when V=10, Y=100, and vice-versa. This transfer function has been implemented in colorimeters, using analog electric circuits. It is used in Hunter Lab - the precursor of CIE Lab.
'Munsell' is the next (1933) transfer function,
and was proposed by Munsell's son (Alexander Ector Orr Munsell) and co-workers.
It is implemented as:
V = sqrt( 1.474*Y - 0.00474*Y^2 )
Y = 50 * ( (1474 - sqrt(1474^2 - 4*4740*V^2)) / 474 )
One readily checks that when V=10, Y=100, and vice-versa. The luminance factor Y is absolute, AKA relative to the perfect reflecting diffuser.
'Priest' and 'Munsell' are included in this package
for historical interest only.
The remaining three define Y as a quintic polynomial in V.
The next one historically - 'MgO' - is implemented as:
Y = (((((8404*V - 210090)*V + 2395100)*V - 2311100)*V + 10000000)*V ) / 10000000
One readily checks that when V=10, Y=102.568. This Y is larger than 100, because the authors decided to make Y relative to a clean surface of MgO, instead of the perfect reflecting diffuser. In their words:
It should be noted that the reflectances indicated are not absolute but relative to magnesium oxide; whereas the maximum at value 10/ was formerly 100 percent, it is now 102.57. Use of this relation facilitates results and also avoids the somewhat dubious conversion to absolute scale, by permitting Y determinations with a MgO standard to be converted directly to Munsell value.
Nowadays, the perfect reflecting diffuser is preferred over MgO.
For users who would like to modify this quintic as little as possible,
with the perfect reflecting diffuser in mind
(going back to 'MUNSELL'),
I offer 'OSA', which is given by this quintic of my own design
Y = (((((8404*V - 210090)*V + 2395100)*V - 2311100)*V + 10000000)*V ) / 10256800
ASTM had a similar modification in mind,
but did it a little differently by scaling each coefficient.
'ASTM' is given by this quintic:
Y = ( ((((81939*V - 2048400)*V + 23352000)*V - 22533000)*V + 119140000)*V ) / 1.e8
One readily checks that when V=10, Y=100 exactly (for both 'OSA' and 'ASTM').
The inverses - from Y to V - of all 3 quintics are implemented as
3 splinefun()s at a large number (about 300) of points.
These inverses are both fast and accurate.
The round-trip Y → V → Y is accurate to 7 digits after the decimal.
The round-trip V → Y → V is accurate to 8 digits after the decimal.
Value
a numeric vector the same length as the input
Note
The quintic functions 'ASTM' and 'OSA' are very close.
They agree at the endpoints 0 and 10 exactly, and the largest difference is near
V=6.767 where they differ by about 0.0007.
Author(s)
Glenn Davis
References
Priest, I. G. Gibson, K. S. and McNicholas, H. J. An Examination of the Munsell Color System. I. Spectral and and Total Reflection and the Munsell Scale of Value. Technologic Papers of the Bureau of Standards, No. 167. pp. 1-33. Washington D.C. 1920.
Munsell, A. E. O., L. L. Sloan, and I. H. Godlove. Neutral Value Scales. I. Munsell Neutral Value Scale. Journal of the Optical Society of America. Vol. 23. Issue 11. pp. 394-411. November 1933.
Newhall, Sidney M., Dorothy Nickerson, Deane B. Judd. Final Report of the O.S.A. Subcommitte on the Spacing of the Munsell Colors. Journal of the Optical Society of America. Vol. 33. No. 7. pp. 385-418. July 1943.
ASTM D 1535-08. Standard Practice for Specifying Color by the Munsell System. 2008
See Also
MunsellToxyY(),
xyYtoMunsell()
Examples
VfromY( c(0,50,100) )
## [1] 0.00000 7.53772 10.00000
Convert XYZ coordinates to Munsell HVC
Description
XYZtoMunsell Convert XYZ coordinates to Munsell HVC, by interpolating over the Munsell renotation data
Usage
XYZtoMunsell( XYZ, ... ) Arguments
XYZ |
a numeric Nx3 matrix with CIE XYZ coordinates in the rows, or a vector that can be converted to such a matrix, by row. The XYZ are for viewing in an environment with Illuminant C. XYZ must be scaled so that Y=100 for the perfect reflecting diffuser. |
... |
other parameters passed to |
Details
the function calls XYZ2xyY() and xyYtoMunsell().
The conversion is done in these steps:
XYZ → xyY using
spacesXYZ::xyYfromXYZ()xyY → HVC using
xyYtoMunsell()and...
Value
an Nx3 matrix with Munsell HVC in the rows.
The rownames are copied from input to output, unless the rownames are NULL
when they are set to the Munsell notations for HVC.
In case of error, it returns NULL.
Author(s)
Jose Gama and Glenn Davis
References
Paul Centore 2014 The Munsell and Kubelka-Munk Toolbox https://www.munsellcolourscienceforpainters.com/MunsellAndKubelkaMunkToolbox/MunsellAndKubelkaMunkToolbox.html
See Also
MunsellToXYZ(),
spacesXYZ::xyYfromXYZ()
Examples
XYZtoMunsell( c(31.0897, 30.6510, 74.613450) )
## H V C
## 5.4PB 6.1/9.4 75.43786 6.117631 9.416488
Plot Curves of Constant Munsell Hue and Chroma
Description
Plot Curves of Constant Munsell Hue and Chroma
Usage
plotLociHC( value=5, hue=seq(2.5,100,by=2.5), chroma='auto', coords='xy',
main="Value %g/", est=FALSE, ... ) Arguments
value |
a Munsell value for which the plot is created.
It must be in the interval (0,10].
|
hue |
a numeric vector for which curves of contant Hue are plotted.
Each of these radial curves starts at Munsell Chroma = |
chroma |
a numeric vector for which ovoids of constant Chroma are plotted.
Each of these ovoids is closed; i.e. goes full circle from Hue=0 to Hue=100.
If |
coords |
either |
main |
a string used to set the main title of the plot.
The optional placeholder |
est |
if |
... |
other arguments passed to the function |
Details
The plot limits (xlim and ylim) are set to include
all points where the Hue radials intersect the Chroma ovoids,
plus the white point.
If value is one of {0.2,0.4,0.6,0.8,1,2,3,4,5,6,7,8,9,10}
then published points from real.dat
are plotted with filled black points (real points),
and extrapolated points from all.dat are drawn with open circles (unreal points).
Value
TRUE for success and FALSE for failure.
Note
The option hcinterp='bicubic' makes fairly smooth ovoids,
and hcinterp='bilinear' makes 40-sided polygons (when coords='xy').
Compare with the plots in
Newhall et. al. (1943),
Judd, et. al. (1956),
and Judd, et. al. (1975) p. 263.
Author(s)
Glenn Davis
References
Newhall, Sidney M., Dorothy Nickerson, Deane B. Judd. Final Report of the O.S.A. Subcommitte on the Spacing of the Munsell Colors. Journal of the Optical Society of America. Vol. 33. No. 7. pp. 385-418. July 1943.
Judd, Deane B. and Günther Wyszecki. Extension of the Munsell Renotation System to Very Dark Colors. Journal of the Optical Society of America. Vol. 46. No. 4. pp. 281-284. April 1956.
Judd, Deane B. and Günther Wyszecki. Color in Business, Science, and Industry. 3rd edition. John Wiley & Sons. 1975.
See Also
MunsellToxyY(),
HueNumberFromString()
Plot Colored Patches for a fixed Munsell Hue
Description
This plot simulates a page from the Munsell Book of Color. The colors are best viewed on a display calibrated for the RGB space given as the second argument.
Usage
plotPatchesH( hue, space='sRGB', adapt='Bradford', background='gray50',
main="Hue %s (H=%g) [%s adapt=%s]",
value=NULL, chroma=NULL, ... ) Arguments
hue |
a Munsell hue for which the plot is created.
It is automatically wrapped to the interval (0,100].
It does not have to be a multiple of 2.5.
|
space |
the name of an installed RGB space.
Spaces |
adapt |
method used to adapt xyY for Illuminant C to xyY for Illuminant D65.
It is passed to |
background |
background color for the plot.
It is passed to |
main |
a string used to set the main title of the plot.
The optional placeholder |
value |
a vector of Munsell Values to use for the plot.
Values must be in the interval [0,10], and in strictly increasing order.
Non-integers, such as 2.5 and 8.5, are valid.
If |
chroma |
a vector of Munsell Chromas to use for the plot.
Chromas must be non-negative and in strictly increasing order.
Odd integers and non-integers are valid.
If |
... |
other arguments passed to the function |
Details
If chroma=NULL,
for the closest discrete Hue in real.dat,
the patches in real.dat are transformed to xyY using simple lookup with no interpolation.
These are then tested against the MacAdam Limits for Illuminant C
using IsWithinMacAdamLimits().
The patches outside the limits are discarded,
and the maximum Chroma of the remaining patches,
which is always an even integer, determines chroma.
Patches inside the MacAdam Limits can still be outside the RGB cube;
those patches are drawn in outline only, and with the clamped RGB coordinates printed inside.
Value
TRUE for success and FALSE for failure.
Author(s)
Glenn Davis
See Also
MunsellToRGB(),
HueNumberFromString(),
IsWithinMacAdamLimits(),
spacesRGB::installRGB()
Round a Given Munsell HVC to the Closest Sample in One or More Books of Samples
Description
The functions in this package compute Munsell HVC coordinates with high precision. When reporting the Munsell notation it is often desirable, for historical consistency or other reasons, to report a notation that is actually appears in one or more published books of Munsell samples. This rounding operation requires exact knowledge of such books. We use a paper by Ferguson, which gives the contents of books on these fields: soil, rocks, beads, and plants. It also includes The New Munsell Student Color Set, see References.
Usage
roundHVC( HVC, books )Arguments
HVC |
a numeric Nx3 matrix with Munsell HVC values in the rows, or a vector that can be converted to such a matrix, by row.
|
books |
a comma-delimted string that specifies one or more books of samples.
The words in the string can be
|
Details
First, the set of samples over all selected books is formed.
Then the closest sample in this set to the given notation is found.
For the color distance, the function
NickersonColorDifference() is used.
Unfortunately, the particular coefficients in this difference equation can lead to large regions
of Munsell color space with exact ties for the two closest samples.
These exact ties make the final result unpredictable and sometime unintuitive.
As a tie-breaker, a very small multiple (1.e-6) of plain
Eucliden distance is added to the Nickerson difference, which has proven effective.
Value
A data.frame with a N rows and these columns:
HVC |
the original Nx3 input matrix HVC. |
ISCC-NBS Name |
the ISCC-NBS Name (the color name) of the given input sample. |
MunsellRounded |
the rounded Munsell notation that is rounded from HVC.
It is guaranteed to be in one of the books given by the argument |
Ferguson Name |
the color name of |
The row names are set to the row names of HVC.
But if these are NULL they are set to the Munsell notation of the input HVC.
Finally, if these row names have duplicates, they are set to 1:N.
Acknowledgements
The conversion of the book data to
Supplement1_3.6.2024.csv was done by Willie Ondricek,
who provided all the motivation for this function.
He also kindly provided photographs of the soil book, and much other material.
Author(s)
Glenn Davis
Source
The data on books of samples is provide in
.../munsellinterpol/inst/extdata/Supplement1_3.6.2024.csv.
This was converted from the original file yjfa_a_11710256_sm0001.docx
which is Online Supplement #1 from Ferguson.
The sample counts in the 5 books are:
| Book | Sample Count |
| Soil | 437 |
| Rock | 115 |
| Bead | 176 |
| Plant | 332 |
| New Munsell Student | 246 |
The union of all 5 books has 869 samples.
References
Ferguson, Jonathan. Munsell notations and color names: Recommendations for archaeological practice. Journal of Field Archaeology. 39:4. 327-335. (2014). Online Supplement #1.
Long, J. T. The New Munsell Student Color Set. New York: Fairchild Books. 2011.
Munsell Color. Munsell Soil-Color Charts. Grand Rapids, MI: 2009.
Munsell Color. Geological Rock-Color Chart. GrandRapids, MI: 2009.
Munsell Color. Munsell Bead Color Book. Grand Rapids, MI: 2012.
Munsell Color. Munsell Color Charts for Plant Tissues. New Windsor, NY: 1977.
Examples
## search the soil book for the best match for 3 samples
roundHVC( c("7.7YR 3.4/6.1", "2.6PB 6.1/4.5", "N 6.6/" ), books='soil' )
## HVC.H HVC.V HVC.C ISCC-NBS Name MunsellRounded Ferguson Name
## 7.7YR 3.4/6.1 17.7 3.4 6.1 strong brown 7.5YR 4/6 Strong brown
## 2.6PB 6.1/4.5 72.6 6.1 4.5 pale blue 5PB 6/1 Bluish gray
## N 6.6/ 0.0 6.6 0.0 light gray N 7/ Light gray
## The middle sample has a poor match, since "purplish-blue" with Chroma=4.5
## is not well-matched by soil color samples.
## Search again, but this time in all 5 books.
roundHVC( c("7.7YR 3.4/6.1", "2.6PB 6.1/4.5", "N 6.6/" ), books='s,b,r,p,n' )
## HVC.H HVC.V HVC.C ISCC-NBS Name MunsellRounded Ferguson Name
## 7.7YR 3.4/6.1 17.7 3.4 6.1 strong brown 7.5YR 4/6 Strong brown
## 2.6PB 6.1/4.5 72.6 6.1 4.5 pale blue 5PB 6/4 Pale blue
## N 6.6/ 0.0 6.6 0.0 light gray N 7/ Light gray
## This time, for the middle sample, a better match was found.
## The other 2 sample are unchanged.
Convert sRGB coordinates to Munsell HVC
Description
Converts non-linear sRGB coordinates to Munsell HVC, by interpolating over the extrapolated Munsell renotation data
Usage
sRGBtoMunsell( sRGB, maxSignal=255, ... ) Arguments
sRGB |
a numeric Nx3 matrix with signal sRGB coordinates in the rows, or a vector that can be converted to such a matrix, by row. These are non-linear signal values, but they are not required to be integers. |
maxSignal |
maximum value of signal sRGB. Other popular values are 1, 100, 1023, and 65535. Even when 1, they are still taken to be non-linear signal values. |
... |
other parameters passed to |
Details
The conversion is done in these steps:
sRGB → XYZ using
spacesXYZ::XYZfromRGB()with the givenmaxSignalXYZ is adapted from Illuminant D65 (from the sRGB standard) to Illuminant C, using
spacesXYZ::adaptXYZ()with the Bradford chromatic adaptation methodXYZ → HVC using
XYZtoMunsell()and the given...
Value
a numeric Nx3 matrix with HVC coordinates in the rows.
The rownames are copied from input to output, unless the rownames are NULL
when they are set to the Munsell notations for HVC.
In case of error, it returns NULL.
Note
The more general function RGBtoMunsell() also performs this conversion.
This function has the advantage that it takes a little less time,
since the CAT (using the Bradford method) is precomputed during
base::.onLoad().
But it has the disadvantage that the chromatic adaptation method cannot be changed.
Author(s)
Jose Gama and Glenn Davis
References
Wikipedia. sRGB. https://en.wikipedia.org/wiki/SRGB.
Paul Centore 2014 The Munsell and Kubelka-Munk Toolbox https://www.munsellcolourscienceforpainters.com/MunsellAndKubelkaMunkToolbox/MunsellAndKubelkaMunkToolbox.html
See Also
RGBtoMunsell(),
XYZtoMunsell(),
spacesXYZ::CAT(),
spacesXYZ::adaptXYZ(),
spacesXYZ::XYZfromRGB()
Examples
sRGBtoMunsell( c(255,45,67) )
## H V C
## 5.4R 5.5/18 5.401135 5.477315 18.01984
sRGBtoMunsell( c(1,0,1), maxSignal=1 )
## H V C
## 8P 6/26 87.98251 5.981297 25.64534
Convert xyY coordinates to Munsell HVC
Description
xyYtoMunsell Convert xyY coordinates to Munsell HVC,
by interpolating over the extrapolated Munsell renotation data.
HVC \to xyY is the forward direction, and xyY \to HVC is the inverse direction.
This inversion requires requires root-finding,
which is done using rootSolve::multiroot().
Usage
xyYtoMunsell( xyY, xyC='NBS', hcinterp='bicubic', vinterp='cubic',
VfromY='ASTM', rtol=1.e-8, atol=1.e-6, warn=TRUE, perf=FALSE ) Arguments
xyY |
a numeric Nx3 matrix with CIE xyY coordinates in the rows, or a vector that can be converted to such a matrix, by row. These are for viewing in an environment with Illuminant C, with Y=100. |
xyC |
a numeric 2-vector with xy chromaticity of Illuminant C.
It can also be one of the strings given in |
hcinterp |
either |
vinterp |
either |
VfromY |
passed as the parameter |
rtol |
relative tolerance passed to |
atol |
absolute tolerance passed to |
warn |
if an xyY cannot be mapped
(usually because the root finder has wandered afar),
its H and V are set to |
perf |
if |
Details
See MunsellToxyY() and the User Guide - Appendix C.
Value
a data.frame with N rows and these columns:
xyY |
The input xyY |
HVC |
the computed HVC. H is automatically wrapped to (0,100]. In case of failure, H and C are set to |
SAMPLE_NAME |
the Munsell notation for HVC, a character vector |
If perf is TRUE then there are these additional columns:
time.elapsed |
elapsed time in seconds. If available, the function |
iterations |
the number of iterations of |
evalations |
the number of forward (HVC → xyY) function evaluations |
estim.precis |
the estimated precision from |
Warning
Even when vinterp='cubic' the function xyY → HVC is not C^1
on the plane V=1.
This is because of a change in Value spacing:
when V\ge1 the Value spacing is 1, but when V\le1 the Value spacing is 0.2.
Author(s)
Jose Gama and Glenn Davis
Source
Paul Centore 2014
The Munsell and Kubelka-Munk Toolbox
https://www.munsellcolourscienceforpainters.com/MunsellAndKubelkaMunkToolbox/MunsellAndKubelkaMunkToolbox.html
https://www.rit.edu/science/munsell-color-lab
https://www.rit-mcsl.org/MunsellRenotation/all.dat
https://www.rit-mcsl.org/MunsellRenotation/real.dat
References
Judd, Deane B. The 1931 I.C.I. Standard Observer and Coordinate System for Colorimetry. Journal of the Optical Society of America. Vol. 23. pp. 359-374. October 1933.
Newhall, Sidney M., Dorothy Nickerson, Deane B. Judd. Final Report of the O.S.A. Subcommitte on the Spacing of the Munsell Colors. Journal of the Optical Society of America. Vol. 33. No. 7. pp. 385-418. July 1943.
Kelly, Kenneth L. Kasson S. Gibson. Dorothy Nickerson. Tristimulus Specification of the Munsell Book of Color from Spectrophometric Measurements National Bureau of Standards RP1549 Volume 31. August 1943.
Judd, Deane B. and Günther Wyszecki. Extension of the Munsell Renotation System to Very Dark Colors. Journal of the Optical Society of America. Vol. 46. No. 4. pp. 281-284. April 1956.
Paul Centore 2014 The Munsell and Kubelka-Munk Toolbox https://www.munsellcolourscienceforpainters.com/MunsellAndKubelkaMunkToolbox/MunsellAndKubelkaMunkToolbox.html
See Also
MunsellToxyY(),
rootSolve::multiroot(),
microbenchmark::get_nanotime()
Examples
xyYtoMunsell(c(0.310897, 0.306510, 74.613450))
## xyY.1 xyY.2 xyY.3 HVC.H HVC.V HVC.C SAMPLE_NAME
## 1 0.310897 0.306510 74.613450 87.541720 8.900000 2.247428 7.5P 8.9/2.2